Руби М. Длинная рука второго закона
Словно вопреки второму закону термодинамики, порядок нередко возникает из хаоса. Новая теоретическая концепция разрешает этот парадокс. Новый взгляд на теорию позволил ученым заполнить этот пробел и убедиться, что второй закон термодинамики справедлив не только для равновесных систем. Однако повсеместное превращение порядка в хаос оставляет достаточно места для очагов самоорганизации...
ОБ АВТОРЕ
Мигель Руби (J. Miguel Rubi) — профессор физики в Барселонском университете. В 2003 г. за вклад в неравновесную термодинамику и теорию стохастических процессов он получил медаль Онсагера (присуждаемую Норвежским научно-техническим университетом) и Гумбольдтовскую премию (присуждаемую немецким фондом Александра фон Гумбольдта).
ПОЛОЖЕНИЯ
• Второй закон термодинамики гласит, что энтропия неизбежна. Но если мир неуклонно стремится к беспорядку, то как объяснить процессы самоорганизации, часто встречающиеся в природе? Все дело в том, что в классической термодинамике рассматриваются системы в состоянии равновесия, которое редко встречается на практике.
• Новый взгляд на теорию позволил ученым заполнить этот пробел и убедиться, что второй закон термодинамики справедлив не только для равновесных систем. Однако повсеместное превращение порядка в хаос оставляет достаточно места для очагов самоорганизации.
• Новый взгляд на теорию позволил ученым заполнить этот пробел и убедиться, что второй закон термодинамики справедлив не только для равновесных систем. Однако повсеместное превращение порядка в хаос оставляет достаточно места для очагов самоорганизации.
ВТОРОЙ ЗАКОН
Второй закон — самый известный из четырех законов термодинамики, науки о тепле и энергии. Если первый закон констатирует, что невозможно получить что-то из ничего, то второй гласит, что нельзя получить что-то из чего-то. Почти во всех процессах часть энергии теряется в виде тепла, поэтому для получения чего-то нужно затратить что-то большее. Такие процессы необратимы: для возврата в исходное состояние нужно затратить дополнительную энергию. Следовательно:
Второй закон — самый известный из четырех законов термодинамики, науки о тепле и энергии. Если первый закон констатирует, что невозможно получить что-то из ничего, то второй гласит, что нельзя получить что-то из чего-то. Почти во всех процессах часть энергии теряется в виде тепла, поэтому для получения чего-то нужно затратить что-то большее. Такие процессы необратимы: для возврата в исходное состояние нужно затратить дополнительную энергию. Следовательно:
-
КПД любого двигателя в принципе не может достичь 100%;
-
тепловые насосы принципиально эффективнее печей, поскольку они не вырабатывают, а перекачивают тепло;
-
очистка памяти компьютера необратима, значит, она сопровождается выделением тепла
Наука принесла человечеству много разочарований. Она ограничила возможности наших технологий, доказав, в частности, что скорость света недостижима, не смогла защитить нас от рака и других болезней и поставила перед лицом таких печальных фактов, как, например, глобальное потепление. Но все вышеперечисленное меркнет перед вторым законом термодинамики, который гласит, что наша Вселенная становится все более беспорядочной, и с этим ничего нельзя сделать. Сама жизнь вносит вклад в неумолимое вырождение мира. Как бы мы ни совершенствовали наши машины, нам не удастся уберечь их от износа и энергетических потерь. Второй закон термодинамики не только разбивает мечту о вечном двигателе, но и предрекает Вселенной тепловую смерть: растратив со временем всю свою энергию, она погрузится в состояние вечного покоя.
По иронии судьбы термодинамика зародилась в середине XIXв., в эпоху технического оптимизма, когда паровые машины изменяли наш мир, а известные физики Рудольф Клаузиус, Николя Сади Карно, Джеймс Джоуль и лорд Кельвин разрабатывали теорию энергии и тепла, чтобы объяснить, как работает паровой двигатель и чем ограничивается его коэффициент полезного действия. Из чисто прикладной науки термодинамика выросла в одну из важнейших отраслей физики и техники. Как общая теория коллективных свойств сложных систем она описывает не только паровые машины, но и колонии бактерий, и устройство компьютерной памяти, и даже черные дыры в космосе. По сути, все такие системы ведут себя одинаково и деградируют в соответствии со вторым законом термодинамики.
Однако, несмотря на практический успех, второй закон термодинамики нередко кажется парадоксальным. Утверждение, что любая система неуклонно деградирует, опровергается многочисленными примерами, поскольку в природе наблюдаются не только разупорядочение и упадок, но также самоорганизация и рост. Кроме того, первоначальный вывод данного закона имеет серьезные теоретические недостатки. Во всяком случае, его не следует применять столь широко, как это практикуется.
Многие ученые, внесшие свой вклад в создание термодинамики, осознавали существующие недостатки и пытались создать более полную теорию. В XX в. над ней работали Ларе Онсагер (Lars Onsager), Илья Пригожий, Сибрен де Гроот (Sybren de Groot), Питер Мазур (Peter Mazur) и другие, но даже их более сложный подход имел ограничения в применении. Лишь недавно нам удалось укрепить основы термодинамики и расширить сферу ее применимости. Мы не только подтвердили, что второй закон универсален, но также выяснили, что он не столь мрачен, как о нем думают.
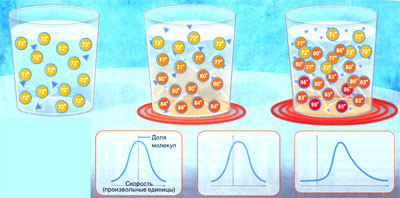
Внимание! Содержимое может быть и горячим, и холодным одновременно!
Понятие температуры кажется простым и универсальным. Тело может быть горячим или холодным, но всегда имеет определенную температуру, правда? Не совсем. Температуру можно приписать лишь тем системам (например, молекулам воды в стакане), которые находятся в рановесии или близки к нему. По мере отклонения системы от равновесия температура становится всё более неопределённой.
РАВНОВЕСИЕ: Вода в стакане принимает комнатуню температуру. Молекулы воды в нём сталкиваются между собой, перераспределяя энергию таким образом, что общее распределение скоростей стабилизируется. Хотя в стакане находятся миллиарды миллиардов молекул, для описания этого распределения достаточно одного числа - значения температуры, и классическая термодинамика здесь вполне применима.
УМЕРЕННОЕ ОТКЛОНЕНИЕ ОТ РАВНОВЕСИЯ: Нагрев воды снизу возмущает равновесия. Но если он не слишком силен, то отдельные слои воды находятся почти в равновесии (локальное равновесие) и воду можно охарактеризовать значением температуры, повышающимся сверху вниз. Здесь применима теория неравновесной термодинамики, разработанная в XX веке.
СИЛЬНОЕ ОТКЛОНЕНИЕ ОТ РАВНОВЕСИЯ: При усилении нагрева отдельные слои воды уже не могут оставаться в равновесии. Молекулы образуют хаотичную мешанину, к которой монятие температуры уже неприменимо. Для описания такой системы необходимо ввести ряд новых переменных и, в самом предельном случае, характеризовать скорости каждой молекулы отдельно. Такая ситуация требует новой теории.
Вне равновесия
Термодинамика — одна из самых трудных для понимания областей физики. И обыватели, и ученые часто используют понятия температуры, давления и энергии, не задумываясь об их точном смысле. Но те, кто проник в глубины теории, четко осознают необходимость осторожного подхода. Ахиллесова пята термодинамики в том, что она, строго говоря, применима только к системам, находящимся в состоянии равновесия, когда масса, энергия и конфигурация системы перестали изменяться. Если поместить рядом два тела с разными температурами, тепло потечет от более нагретого тела к более холодному. Этот поток прекратится только тогда, когда температуры обоих тел сравняются, и тела окажутся в состоянии теплового равновесия. После этого изменения прекратятся.
Рассмотрим пример с кубиком льда в стакане воды. Лед в воде тает, и вся вода в стакане принимает однородную, более низкую температуру. Рассматривая процесс на молекулярном уровне, мы обнаружим беспорядочное движение молекул, постоянно сталкивающихся друг с другом. Когда вода находится в состоянии равновесия, молекулы движутся так, что статистически система пребывает в покое: если одни молекулы ускоряются, то другие замедляются, и общее распределение скоростей остается неизменным. Это распределение описывает температура, само понятие которой имеет смысл только применительно к системам, находящимся в равновесии или почти в равновесии.
Таким образом, термодинамика имеет дело только с состоянием покоя, и время в ней не имеет значения. В реальном мире время играет важную роль, и все находится в непрерывном движении. Может показаться неожиданным, что классическая термодинамика применима только к системам в состоянии равновесия: ведь на уроках физики ее уравнения используются для расчета КПД динамических систем, таких как автомобильные двигатели. Однако в данном случае делается неявное допущение: динамический процесс аппроксимируется идеализированной последовательностью равновесных состояний. Иными словами, мы представляем себе систему, которая всегда находится в равновесии, даже если это равновесие изменяется с течением времени. Вычисленное таким образом значение будет предельным: КПД реального двигателя будет несколько ниже, поскольку он работает в неравновесном режиме.
Второй закон термодинамики объясняет, почему последовательность равновесных состояний может быть необратимой, и почему система не может вернуться в первоначальное состояние, не получив энергию из окружающей среды. Растаявший кубик льда не сформируется вновь сам собой: чтобы получить лед, нужно поместить воду в морозильник и затратить энергию. В качестве меры необратимости второй закон термодинамики вводит ключевое понятие — энтропию. Обычно ее описывают как степень неупорядоченности системы, но такое представление, как будет показано ниже, может ввести в заблуждение. Количественно энтропия определяется как отношение количества тепла, участвующего в теплообмене, к температуре. В изолированной системе она не может уменьшаться. Например, в обычном двигателе используется поток тепла от более горячего резервуара к более холодному, причем оба резервуара представляют собой большие массы, внешние по отношению к механизму двигателя. Если температуры резервуаров постоянны, а трение в механизме отсутствует, рабочий цикл двигателя осуществляется полностью обратимым образом. При этом энтропия остается неизменной. В реальном двигателе рабочий цикл необратим, и общая энтропия возрастает. В конце концов двигатель расходует всю доступную энергию, поток тепла прекращается, и энтропия достигает максимального значения. В этот момент оба тепловых резервуара и двигатель оказываются в тепловом равновесии друг с другом, и в дальнейшем все остается стабильным.
Поскольку классическая термодинамика основывается на допущении о равновесности состояний, применимость ее второго закона ограничена. Если система не находится в равновесии, для нее нельзя даже определить энтропию и температуру. Более того, многие системы не могут быть представлены моделью тепловой машины. Примером может служить Вселенная: если пространство расширяется, энтропия может возрастать неограниченно, так что Вселенная стремится к равновесному состоянию, но не может достичь его (см.: Кэрролл Ш. Происхождение стрелы времени» // ВМН, № 9, 2008). Общим для этих систем является то, что они не находятся в равновесии и даже не близки к нему.
Порядок из хаоса
Поведение неравновесных систем не поддается описанию в рамках классической термодинамики и вступает в противоречие с представлением о неуклонном росте беспорядка в природе. Рассмотрим электрический тостер. Его спираль нагревается потому, что проволока оказывает сопротивление протеканию электрического тока. Второй закон термодинамики утверждает, что данный процесс необратим: невозможно заставить тостер «разжаривать» хлеб обратно и за счет этого вырабатывать электроэнергию.
Однако можно создать разность температур между концами спирали тостера и вывести систему из равновесия. При этом она действительно начнет вырабатывать электроэнергию. На таком обращении основано действие термопары — устройства, применяемого для измерения температуры или выработки электроэнергии.
Другой пример — обратный осмос, который используется для опреснения морской воды. При обычном осмосе различие в концентрациях соли по разные стороны мембраны создает разность давлений, под действием которой вода течет в сторону большей солености и разбавляет раствор. В итоге система достигает равновесия. При обратном осмосе внешнее давление поддерживает систему в неравновесном состоянии и заставляет воду течь в сторону с меньшей соленостью, т.е. опресняться.
В обоих примерах ключевую роль играют так называемые соотношения взаимности, сформулированные лауреатом Нобелевской премии по химии 1968 г. Ларсом Онсагером. Симметричность рассмотренных процессов отражает обратимость законов, управляющих движением частиц в системе: эти законы действуют одинаково как при прямом, так и при обратном течении времени. Необратимость, наблюдаемая на макроскопическом уровне, возникает только при рассмотрении больших совокупностей частиц.
Открытие соотношений взаимности изменило представление физиков о равновесии. Они привыкли считать его наиболее упорядоченным состоянием. Несмотря на то что молекулы могут вести себя максимально беспорядочно, система в целом спокойна, симметрична и упорядочена. Однако соотношения взаимности показывают, что и неравновесная система может быть высоко упорядоченной. Регулярность, симметрия и островки покоя могут существовать и в далеких от равновесия состояниях.
Другой классический пример — тонкий слой жидкости, нагреваемый снизу. В нем существует поток тепла, направленный снизу вверх и создающий в слое градиент температуры. Чем больше градиент, тем больше отклонение от равновесия. При небольших градиентах жидкость остается неподвижной, но при более значительных в ней возникают конвективные потоки, причем не хаотические, а упорядоченные.
В жидкости формируются маленькие шестиугольные ячейки, как если бы она была кристаллом. При еще больших градиентах движение становится турбулентным. Это явление, названное проблемой Бенара, показывает, что по мере отклонения системы от равновесия порядок может превращаться в хаос, а хаос — снова в порядок.
Рассмотрим еще один пример. Возьмем покоящуюся жидкость: она изотропна, ее свойства одинаковы во всех направлениях. Теперь заставим жидкость течь через металлическую сетку с определенной скоростью. Хотя за сеткой поток станет турбулентным, жидкость будет двигаться в одном направлении и перестанет быть изотропной. Если мы начнем увеличивать скорость потока, турбулентность в нем будет возрастать и в конце концов достигнет уровня, при котором жидкость уже не будет течь строго в одном направлении и вновь станет изотропной. Таким образом, в ходе эксперимента жидкость сначала перейдет из изотропного состояния в анизотропное, а затем обратно в изотропное.
Классическая термодинамика не в состоянии описать перечисленные явления, и ее ограниченность с каждым годом все сильнее мешает ученым. Исследователи в области молекулярной биологии и нанотехнологии сталкиваются с большим разнообразием организованных, но постоянно изменяющихся структур. Для их изучения требуется теория неравновесной термодинамики.
Разработка новой теории началась с концепции локального равновесия. Некоторые части неравновесной в целом системы могут быть в равновесии. Представьте себе, что вы перемешиваете коктейль палочкой. Ее движение нарушает равновесие, но если присмотреться внимательнее, то можно увидеть малые объемы жидкости, сохраняющие внутреннюю когерентность. Они остаются в равновесии, пока силы, действующие на систему, не слишком велики, а свойства жидкости почти не меняются на малых расстояниях. К таким островкам равновесия применимы понятия температуры и энтропии, хотя их численные значения у каждого островка свои.
Если нагревать один конец металлического стержня, тепло потечет к его противоположному концу. Разность температур между концами стержня действует как движущая сила потока. То же самое происходит с каплей чернил в воде. Здесь движущей силой служит разность концентраций, заставляющая чернила распространяться в окружающую воду, пока она не станет равномерно окрашенной. Эти силы линейны: поток тепла пропорционален разности температур, а поток частиц — разности концентраций, причем линейная пропорциональность сохраняется и при больших значениях сил, действующих на систему. Даже во многих турбулентных потоках внутренние сдвиговые напряжения в жидкости пропорциональны градиентам скорости. Для таких случаев Онсагер и другие ученые разработали теорию неравновесной термодинамики и показали, что для них второй закон термодинамики остается в силе.
Но когда названные условия не соблюдаются, эта теория терпит фиаско. Скажем, при химической реакции одно вещество внезапно превращается в другое, и такое резкое изменение описывается нелинейным уравнением. Другой пример — системы настолько малые, что их поведение определяется хаотическим движением молекул, которое вызывает сильное изменение свойств на малых расстояниях. Именно такие флуктуации оказывают основное влияние на процессы, протекающие в малых системах, например при конденсации водяного пара или при переносе ионов через белковые каналы в клеточных мембранах. В таких системах невозможно четко определить температуру и энтропию. Можно ли в этих случаях считать несостоятельность теории опровержением второго закона?
В последние годы мы с Давидом Ригуэрой (David Riguera) из Барселонского университета и Хосе Вила-ром (Jose M. G. Vilar) из Института Слоуна-Кеттеринга распространили термодинамическую теорию и на эти случаи. Наше восприятие внезапности зависит от масштаба времени. Анализируя с виду мгновенный химический процесс методом замедленной съемки, можно увидеть, что на самом деле превращение происходит постепенно.
Фокус в том, чтобы проследить промежуточные этапы реакции, используя дополнительные переменные помимо применяемых в классической термодинамике. В такой расширенной сетке координат система сохраняет локальное термодинамическое равновесие в течение всего процесса. Дополнительные переменные обогащают поведение системы и определяют энергетический ландшафт, по которому она движется, словно турист в горах. Долины соответствуют пониженной энергии и иногда представляют собой молекулярный хаос, а иногда — молекулярную упорядоченность. Система может осесть в одной из таких долин, но внешние силы способны перебросить ее в другую: из хаоса в порядок или наоборот.
Рассмотрим теперь проблему флуктуации. Нарушаются ли законы термодинамики в очень маленьких системах? Простой эксперимент показывает, что не нарушаются: если мы подбросим монету всего несколько раз, то может оказаться, что во всех случаях выпадет «орел». Но с увеличением числа бросков результат неизбежно будет приближаться к среднему. Природа «подбрасывает монеты» очень часто. Если в сосуде всего несколько частиц, то они будут сталкиваться лишь изредка, и различие в их скоростях долгое время будет сохраняться.
Но даже системы, которые кажутся малыми, состоят из гораздо большего числа частиц, поэтому столкновения происходят в них намного чаще, а скорость частиц стремится к среднему (хотя и немного флуктуирующему) значению. Несмотря на то что отдельные единичные события могут оказаться совершенно непредсказуемыми, множество событий характеризуется некоей регулярностью. Поэтому такие величины, как плотность, могут флуктуировать, но их среднее значение предсказуемо. Поэтому второй закон термодинамики правит и в мире малых систем.
От паровых машин к молекулярным двигателям
Создателей термодинамики вдохновляли паровые машины, а сегодня она развивается благодаря изучению крошечных молекулярных двигателей в живых клетках. И хотя размеры этих систем несопоставимы, они выполняют одну и ту же функцию — преобразовывают энергию в движение. В частности, молекулы АТФ поставляют «топливо» молекулам миозина в мышечной ткани, заставляя их двигаться вдоль актиновых нитей, сокращая мышечные волокна, к которым они прикреплены. Другие двигатели питаются энергией света, различием концентраций протонов или разностью температур. Химическая энергия заставляет ионы проходить через каналы клеточной мембраны из области с меньшей концентрацией в область с более высокой, т.е. в направлении, противоположном тому, в котором они двигались бы в отсутствие активного движущего механизма.
Сходство между большими и малыми машинами очень велико. Флуктуации химической энергии влияют на молекулярный двигатель так же, как случайные изменения подачи топлива на автомобильный мотор. Поэтому давнюю традицию применения термодинамики к большим машинам можно распространить и на малые. У физиков есть и другие математические инструменты для анализа таких систем, но их применение часто связано со многими трудностями. Так, для решения уравнений, описывающих поток жидкости, требуются точно задать условия на границе системы, а это очень непростая задача, если граница отличается большой нерегулярностью. Термодинамика позволяет намного упростить вычисления, что уже дало свои результаты. Мы с Сигне Кьельструпом (Signe Kjelstrup) и Диком Бедо (Dick Bedeaux) из Норвежского научно-технического университета обнаружили, что роль тепла в работе ионных каналов недооценивалась.
Короче говоря, мы с коллегами показали, что возникновение порядка из хаоса отнюдь не противоречит второму закону термодинамики и прекрасно укладывается в расширенную версию теории. Сейчас мы стоим на пороге практического применения новых знаний. Проект вечного двигателя так и остается неосуществимым, и в итоге мы неизбежно проиграем битву против беспорядка. Но второй закон не постулирует монотонного вырождения и благополучно уживается со спонтанным возникновением упорядоченности и спонтанным усложнением.
Перевод: И.Е. Сацевич
Дополнительная литература
• Nonequilibrium Thermodynamics. S. R. de Groot and P. Mazur. Dover, 1984.
Thermodynamics "beyond" Local Equilibrium. Jose M. G. Vilar and J. Miguel Rubi in Proceedings of the National Academy of Sciences USA, Vol. 98, No. 20, pages 11081-11084; September 25, 2001. http:// arxiv.org/abs/cond-mat/0110614
• Active Transport: a Kinetic Description Based on Thermodynamic Grounds. Signe Kjelstrup, J. Miguel Rubi and Dick Bedeaux in Journal of Theoretical Biology, Vol. 234, No. 1, pages 7-12; May 7, 2005. http://arxiv.org/abs/cond-mat/0412493
• The Mesoscopic Dynamics of Thermodynamic Systems. David Reguera, J.Miguel Rubi and Jose M. G. Vilar in Journal of Physical Chemistry B, Vol. 109, No. 46, pages 21502-21515; November 24, 2005. http://arxiv.org/abs/cond-mat/0511651
Thermodynamics "beyond" Local Equilibrium. Jose M. G. Vilar and J. Miguel Rubi in Proceedings of the National Academy of Sciences USA, Vol. 98, No. 20, pages 11081-11084; September 25, 2001. http:// arxiv.org/abs/cond-mat/0110614
• Active Transport: a Kinetic Description Based on Thermodynamic Grounds. Signe Kjelstrup, J. Miguel Rubi and Dick Bedeaux in Journal of Theoretical Biology, Vol. 234, No. 1, pages 7-12; May 7, 2005. http://arxiv.org/abs/cond-mat/0412493
• The Mesoscopic Dynamics of Thermodynamic Systems. David Reguera, J.Miguel Rubi and Jose M. G. Vilar in Journal of Physical Chemistry B, Vol. 109, No. 46, pages 21502-21515; November 24, 2005. http://arxiv.org/abs/cond-mat/0511651






 Издательство «Свиньин и сыновья» выпустило несколько сотен самых разных по жанру, объему и авторам, но неизменно высококультурных изданий
Издательство «Свиньин и сыновья» выпустило несколько сотен самых разных по жанру, объему и авторам, но неизменно высококультурных изданий





